史瓦西半径公式

史瓦西半径公式

史瓦西半径公式（Schwarzschild radius），又称史瓦西半径、引力半径，是卡尔·史瓦西在1916年得出的公式，用于描述黑洞的视界半径。视界是黑洞周围的一个边界，任何物体一旦进入该边界，将永远无法逃离，包括光。

史瓦西半径公式为：

$$r_s = \frac{2GM}{c^2}$$

其中：

• (r_s) 是史瓦西半径
• (G) 是万有引力常数
• (M) 是黑洞的质量
• (c) 是光速

史瓦西半径与黑洞的质量成正比，质量越大，史瓦西半径越大。黑洞的视界就是史瓦西半径。

史瓦西半径公式的推导

史瓦西半径公式可以从史瓦西度规推导出来。史瓦西度规是描述黑洞周围时空性质的度规。史瓦西度规为：

$$ds^2 = \left(1 - \frac{2GM}{rc^2}\right)dt^2 - \left(1 - \frac{2GM}{rc^2}\right)^{-1}dr^2 - r^2d\Omega^2$$

其中：

• (ds) 是时空间隔
• (dt) 是时间间隔
• (dr) 是径向间隔
• (d\Omega^2) 是球面角元
• (G) 是万有引力常数
• (M) 是黑洞的质量
• (c) 是光速
• (r) 是径向坐标

史瓦西半径就是史瓦西度规中出现的分母为零的点。即：

$$1 - \frac{2GM}{rc^2} = 0$$

即：

$$r = \frac{2GM}{c^2}$$

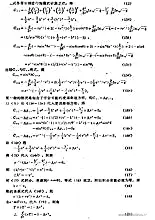
史瓦西半径公式的意义

史瓦西半径公式具有重要的物理意义。它表明，任何物体一旦进入黑洞的视界，将永远无法逃离，包括光。史瓦西半径公式也用于计算黑洞的表面重力。黑洞的表面重力为：

$$g = \frac{GM}{r_s^2}$$

其中：

• (g) 是黑洞的表面重力
• (G) 是万有引力常数
• (M) 是黑洞的质量
• (r_s) 是黑洞的史瓦西半径

史瓦西半径公式在天文物理学中有着广泛的应用。它用于研究黑洞的性质，以及黑洞对周围时空的影响。