角平分线的性质

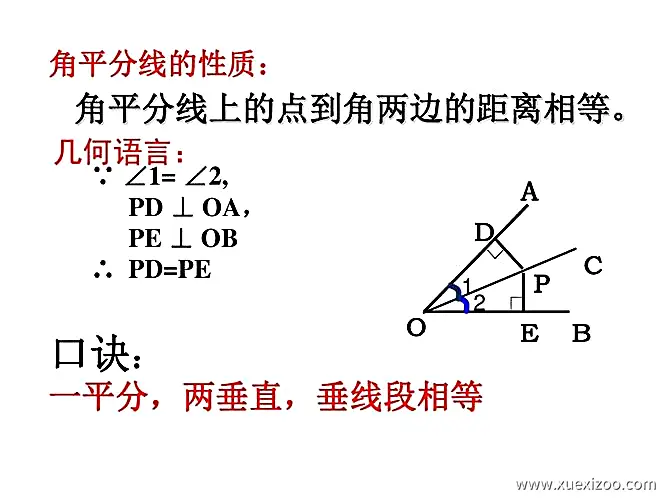
角平分线的性质

1. 角平分线将角等分为两个相等的部分。
2. 角平分线垂直于角的两边。
3. 角平分线将角内的任意一点到两边的距离相等。

证明：

1. 假设∠ABC 是任意角，AD 是其角平分线。那么，∠BAD = ∠CAD。
2. 在△ABD 和 △ACD 中，AD = AD（公共边），∠BAD = ∠CAD（已知），AB = AC（因为 AD 是角平分线）。因此，△ABD ≌ △ACD（SAS）。
3. 由于 △ABD ≌ △ACD，因此 BD = CD（对应边相等）。
4. 又因为 AD ⊥ BC，因此 BD ⊥ BC，CD ⊥ BC。
5. 因此，角平分线 AD 垂直于角的两边。
6. 设 P 是角平分线 AD 上的任意一点。那么，PA = PB（因为 PA 和 PB 是等腰三角形 △APB 的两边）。
7. 同理，PA = PC（因为 PA 和 PC 是等腰三角形 △APC 的两边）。
8. 因此，角平分线将角内的任意一点到两边的距离相等。

应用：

1. 角平分线可以用来将一个角等分为两个相等的部分。
2. 角平分线可以用来构造等腰三角形。
3. 角平分线可以用来构造正方形和正多边形。
4. 角平分线可以用来求解几何问题。