高中数学诱导公式大全
高中数学诱导公式大全
诱导公式是证明某些数学命题或公式时常用到的一种方法。它可以通过数学归纳法来证明。数学归纳法的步骤如下:
- 证明命题或公式对于某个初始值成立。
- 假设命题或公式对于某个值成立。
- 证明命题或公式对于该值的下一个值也成立。
- 得出结论:命题或公式对于所有值都成立。
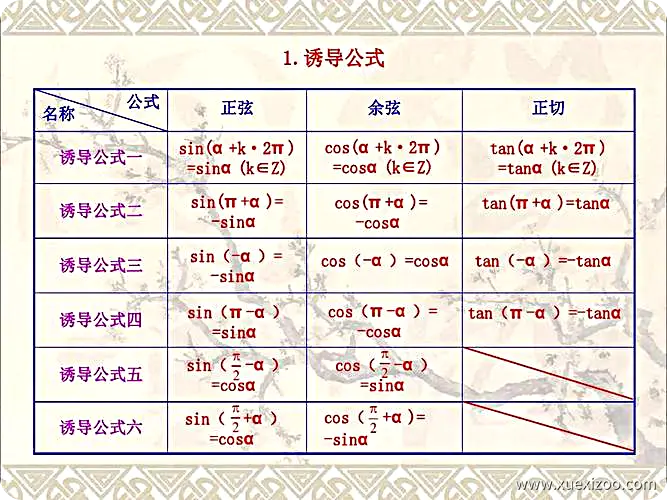
以下是高中数学中常见的诱导公式大全:
- 算术级数求和公式
$$S_n = \frac{n}{2}(a_1 + a_n)$$
其中,$a_1$是算术级数的第一项,$a_n$是算术级数的第$n$项,$S_n$是算术级数的前$n$项和。
- 几何级数求和公式
$$S_n = \frac{a_1(1 - r^n)}{1 - r}$$
其中,$a_1$是几何级数的第一项,$r$是几何级数的公比,$S_n$是几何级数的前$n$项和。
- 二项式定理
$$(a + b)^n = \sum_{k=0}^n \binom{n}{k} a^{n-k} b^k$$
其中,$\binom{n}{k}$是二项式系数,$a$和$b$是二项式展开式中的变量,$n$是二项式展开式的次数。
- 棣莫弗定理
$$(\cos \theta + i \sin \theta)^n = \cos n\theta + i \sin n\theta$$
其中,$\theta$是角,$i$是虚数单位,$n$是幂指数。
- 泰勒级数
$$f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x - a)^n$$
其中,$f(x)$是函数,$a$是展開點,$f^{(n)}(a)$是$f(x)$在$x=a$处的$n$阶导数,$n!$是階乘。
- 傅里叶级数
$$f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty (a_n \cos nx + b_n \sin nx)$$
其中,$a_0, a_n, b_n$是傅里叶系数,$x$是自变量。
- 拉普拉斯变换
$$F(s) = \int_0^\infty e^{-st} f(t) dt$$
其中,$f(t)$是時間函數,$s$是複變變數,$F(s)$是拉普拉斯變換。
- 反拉普拉斯变换
$$f(t) = \frac{1}{2\pi i} \int_{\gamma - i\infty}^{\gamma + i\infty} e^{st} F(s) ds$$
其中,$F(s)$是拉普拉斯變換,$f(t)$是時間函數,$\gamma$是實數。
诱导公式在高中数学中有着广泛的应用,它们可以帮助我们证明许多重要的数学命题和公式,从而加深我们对数学的理解。
作者:小龙人
链接:https://www.xuexizoo.com/article/1759808063168069895.html
文章版权归作者所有,未经允许请勿转载。如有侵权,请发邮件联系管理员进行处理,邮箱地址:121671486@qq.com